1. 漏斗图（funnel plot）：是最常见的识别发表偏倚的方法。它是以纳入meta分析的各研究的效应量估计值（如RR、OR、MD等）作为横坐标（X轴），以每个研究的效应量标准误（standard error，SE）或其对数值作为纵坐标（Y轴）绘制的散点图，其原理是基于效应量估计值的精度随样本量的增加而增加，其宽度随精度的增加而变窄，最后趋近于点状，其形状类似一个对称倒置的漏斗，故称为漏斗图，即小样本研究通常会因精度低分散在漏斗图的底部，而样本量大的研究，精度高，则分布在漏斗图的顶部且向中间集中。因此，如果meta分析不存在发表偏倚，漏斗图会像呈现出对称的倒置漏斗形；如果存在发表偏倚，则漏斗图呈现明显的不对称或不完整。

2. 失安全数（Fail-safe number，N_fs）：meta分析中另外一个常用来识别和评价发表偏倚的方法。它是指推翻或逆转当前合并结论的结果所需的阴性研究的报告数。失效安全数越大，表明meta分析的结果越稳定，发表偏倚对结果的影响就越小，结论被推翻的可能性就越小。P为0.05和0.01时的失效安全数计算公式如下：

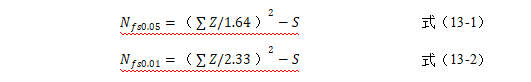
其中，Z为各独立独立研究的Z值，S为纳入研究的个数。

除了漏斗图和失安全数，也可以进行Egger回归或Begger分析来评估发表偏倚。